std.math

Source:
std/math.d

const real E;

const real LOG2T;

log₂10

const real LOG2E;

log₂e

const real LOG2;

log₁₀2

const real LOG10E;

log₁₀e

const real LN2;

ln 2

const real LN10;

ln 10

const real PI;

const real PI_2;

π / 2

const real PI_4;

π / 4

const real M_1_PI;

1 / π

const real M_2_PI;

2 / π

const real M_2_SQRTPI;

2 / √π

const real SQRT2;

√2

const real SQRT1_2;

√½

real abs(real x); long abs(long x); int abs(int x); real abs(creal z); real abs(ireal y);

Calculates the absolute value

For complex numbers, abs(z) = sqrt( z.re² + z.im² ) = hypot(z.re, z.im).

creal conj(creal z); ireal conj(ireal y);

Complex conjugate

conj(x + iy) = x - iy

Note that z * conj(z) = z.re² - z.im² is always a real number

real cos(real x);

Returns cosine of x. x is in radians.

Special Values
x	cos(x)	invalid?
NAN	NAN	yes
±∞	NAN	yes

BUGS:
Results are undefined if |x| >= 2⁶⁴.

real sin(real x);

Returns sine of x. x is in radians.

Special Values
x	sin(x)	invalid?
NAN	NAN	yes
±0.0	±0.0	no
±∞	NAN	yes

BUGS:
Results are undefined if |x| >= 2⁶⁴.

creal sin(creal z); ireal sin(ireal y);

sine, complex and imaginary

sin(z) = sin(z.re)*cosh(z.im) + cos(z.re)*sinh(z.im)i

If both sin(θ) and cos(θ) are required, it is most efficient to use expi(θ).

creal cos(creal z); real cos(ireal y);

cosine, complex and imaginary

cos(z) = cos(z.re)*cosh(z.im) - sin(z.re)*sinh(z.im)i

real tan(real x);

Returns tangent of x. x is in radians.

Special Values
x	tan(x)	invalid?
NAN	NAN	yes
±0.0	±0.0	no
±∞	NAN	yes

real acos(real x);

Calculates the arc cosine of x, returning a value ranging from 0 to π.

Special Values
x	acos(x)	invalid?
>1.0	NAN	yes
<-1.0	NAN	yes
NAN	NAN	yes

real asin(real x);

Calculates the arc sine of x, returning a value ranging from -π/2 to π/2.

Special Values
x	asin(x)	invalid?
±0.0	±0.0	no
>1.0	NAN	yes
<-1.0	NAN	yes

real atan(real x);

Calculates the arc tangent of x, returning a value ranging from -π/2 to π/2.

Special Values
x	atan(x)	invalid?
±0.0	±0.0	no
±∞	NAN	yes

real atan2(real y, real x);

Calculates the arc tangent of y / x, returning a value ranging from -π to π.

Special Values
y	x	atan(y, x)
NAN	anything	NAN
anything	NAN	NAN
±0.0	>0.0	±0.0
±0.0	+0.0	±0.0
±0.0	<0.0	±π
±0.0	-0.0	±π
>0.0	±0.0	π/2
<0.0	±0.0	-π/2
>0.0	∞	±0.0
±∞	anything	±π/2
>0.0	-∞	±π
±∞	∞	±π/4
±∞	-∞	±3π/4

real cosh(real x);

Calculates the hyperbolic cosine of x.

Special Values
x	cosh(x)	invalid?
±∞	±0.0	no

real sinh(real x);

Calculates the hyperbolic sine of x.

Special Values
x	sinh(x)	invalid?
±0.0	±0.0	no
±∞	±∞	no

real tanh(real x);

Calculates the hyperbolic tangent of x.

Special Values
x	tanh(x)	invalid?
±0.0	±0.0	no
±∞	±1.0	no

real acosh(real x);

Calculates the inverse hyperbolic cosine of x.

Mathematically, acosh(x) = log(x + sqrt( x*x - 1))

Special Values
x	acosh(x)
NAN	NAN
<1	NAN
1	0
+∞	+∞

real asinh(real x);

Calculates the inverse hyperbolic sine of x.

Mathematically,

  asinh(x) =  log( x + sqrt( x*x + 1 )) // if x >= +0
  asinh(x) = -log(-x + sqrt( x*x + 1 )) // if x <= -0

Special Values
x	asinh(x)
NAN	NAN
±0	±0
±∞	±∞

real atanh(real x);

Calculates the inverse hyperbolic tangent of x, returning a value from ranging from -1 to 1.

Mathematically, atanh(x) = log( (1+x)/(1-x) ) / 2

Special Values
x	acosh(x)
NAN	NAN
±0	±0
-∞	-0

long rndtol(real x);

Returns x rounded to a long value using the current rounding mode. If the integer value of x is greater than long.max, the result is indeterminate.

real rndtonl(real x);

Returns x rounded to a long value using the FE_TONEAREST rounding mode. If the integer value of x is greater than long.max, the result is indeterminate.

float sqrt(float x); double sqrt(double x); real sqrt(real x);

Compute square root of x.

Special Values
x	sqrt(x)	invalid?
-0.0	-0.0	no
<0.0	NAN	yes
+∞	+∞	no

real exp(real x);

Calculates ex.

Special Values
x	ex
+∞	+∞
-∞	+0.0
NAN	NAN

real expm1(real x);

Calculates the value of the natural logarithm base (e) raised to the power of x, minus 1.

For very small x, expm1(x) is more accurate than exp(x)-1.

Special Values
x	ex-1
±0.0	±0.0
+∞	+∞
-∞	-1.0
NAN	NAN

real exp2(real x);

Calculates 2x.

Special Values
x	exp2(x)
+∞	+∞
-∞	+0.0
NAN	NAN

creal expi(real y);

Calculate cos(y) + i sin(y).

On many CPUs (such as x86), this is a very efficient operation; almost twice as fast as calculating sin(y) and cos(y) separately, and is the preferred method when both are required.

real frexp(real value, out int exp);

Separate floating point value into significand and exponent.

Returns:
Calculate and return x and exp such that value =x*2exp and .5 <= |x| < 1.0

x has same sign as value.

Special Values
value	returns	exp
±0.0	±0.0	0
+∞	+∞	int.max
-∞	-∞	int.min
±NAN	±NAN	int.min

int ilogb(real x);

Extracts the exponent of x as a signed integral value.

If x is not a special value, the result is the same as .

Special Values
x	ilogb(x)	Range error?
0	FP_ILOGB0	yes
±∞	int.max	no
NAN	FP_ILOGBNAN	no

real ldexp(real n, int exp);

Compute n * 2exp

References:
frexp

real log(real x);

Calculate the natural logarithm of x.

Special Values
x	log(x)	divide by 0?	invalid?
±0.0	-∞	yes	no
<0.0	NAN	no	yes
+∞	+∞	no	no

real log10(real x);

Calculate the base-10 logarithm of x.

Special Values
x	log10(x)	divide by 0?	invalid?
±0.0	-∞	yes	no
<0.0	NAN	no	yes
+∞	+∞	no	no

real log1p(real x);

Calculates the natural logarithm of 1 + x.

For very small x, log1p(x) will be more accurate than log(1 + x).

Special Values
x	log1p(x)	divide by 0?	invalid?
±0.0	±0.0	no	no
-1.0	-∞	yes	no
<-1.0	NAN	no	yes
+∞	-∞	no	no

real log2(real x);

Calculates the base-2 logarithm of x: log₂x

Special Values
x	log2(x)	divide by 0?	invalid?
±0.0	-∞	yes	no
<0.0	NAN	no	yes
+∞	+∞	no	no

real logb(real x);

Extracts the exponent of x as a signed integral value.

If x is subnormal, it is treated as if it were normalized. For a positive, finite x:

1 <= x * FLT_RADIX-logb(x) < FLT_RADIX

Special Values
x	logb(x)	divide by 0?
±∞	+∞	no
±0.0	-∞	yes

real modf(real x, ref real i);

Calculates the remainder from the calculation x/y.

Returns:
The value of x - i * y, where i is the number of times that y can be completely subtracted from x. The result has the same sign as x.

Special Values
x	y	modf(x, y)	invalid?
±0.0	not 0.0	±0.0	no
±∞	anything	NAN	yes
anything	±0.0	NAN	yes
!=±∞	±∞	x	no

real scalbn(real x, int n);

Efficiently calculates x * 2n.

scalbn handles underflow and overflow in the same fashion as the basic arithmetic operators.

Special Values
x	scalb(x)
±∞	±∞
±0.0	±0.0

real cbrt(real x);

Calculates the cube root of x.

Special Values
x	cbrt(x)	invalid?
±0.0	±0.0	no
NAN	NAN	yes
±∞	±∞	no

real fabs(real x);

Returns |x|

Special Values
x	fabs(x)
±0.0	+0.0
±∞	+∞

real hypot(real x, real y);

Calculates the length of the hypotenuse of a right-angled triangle with sides of length x and y. The hypotenuse is the value of the square root of the sums of the squares of x and y:

sqrt( + )

Note that hypot(x, y), hypot(y, x) and hypot(x, -y) are equivalent.

Special Values
x	y	hypot(x, y)	invalid?
x	±0.0	\|x\|	no
±∞	y	+∞	no
±∞	NAN	+∞	no

real erf(real x);

Returns the error function of x.

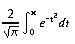
real erfc(real x);

Returns the complementary error function of x, which is 1 - erf(x).

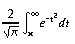
real lgamma(real x);

Natural logarithm of gamma function.

Returns the base e (2.718...) logarithm of the absolute value of the gamma function of the argument.

For reals, lgamma is equivalent to log(fabs(gamma(x))).

Special Values
x	lgamma(x)	invalid?
NAN	NAN	yes
integer <= 0	+∞	yes
±∞	+∞	no

real tgamma(real x);

The Gamma function, Γ(x)

Γ(x) is a generalisation of the factorial function to real and complex numbers. Like x!, Γ(x+1) = x*Γ(x).

Mathematically, if z.re > 0 then Γ(z) = ∫₀^∞ t^z-1e^-t dt

Special Values
x	Γ(x)	invalid?
NAN	NAN	yes
±0.0	±∞	yes
integer >0	(x-1)!	no
integer <0	NAN	yes
+∞	+∞	no
-∞	NAN	yes

References:
http://en.wikipedia.org/wiki/Gamma_function, http://www.netlib.org/cephes/ldoubdoc.html#gamma

real ceil(real x);

Returns the value of x rounded upward to the next integer (toward positive infinity).

real floor(real x);

Returns the value of x rounded downward to the next integer (toward negative infinity).

real nearbyint(real x);

Rounds x to the nearest integer value, using the current rounding mode.

Unlike the rint functions, nearbyint does not raise the FE_INEXACT exception.

real rint(real x);

Rounds x to the nearest integer value, using the current rounding mode. If the return value is not equal to x, the FE_INEXACT exception is raised. nearbyint performs the same operation, but does not set the FE_INEXACT exception.

long lrint(real x);

Rounds x to the nearest integer value, using the current rounding mode.

This is generally the fastest method to convert a floating-point number to an integer. Note that the results from this function depend on the rounding mode, if the fractional part of x is exactly 0.5. If using the default rounding mode (ties round to even integers) lrint(4.5) == 4, lrint(5.5)==6.

real round(real x);

Return the value of x rounded to the nearest integer. If the fractional part of x is exactly 0.5, the return value is rounded to the even integer.

long lround(real x);

Return the value of x rounded to the nearest integer.

If the fractional part of x is exactly 0.5, the return value is rounded away from zero.

Note:
Not supported on windows

real trunc(real x);

Returns the integer portion of x, dropping the fractional portion.

This is also known as "chop" rounding.

real remainder(real x, real y); real remquo(real x, real y, out int n);

Calculate the remainder x REM y, following IEC 60559.

REM is the value of x - y * n, where n is the integer nearest the exact value of x / y. If |n - x / y| == 0.5, n is even. If the result is zero, it has the same sign as x. Otherwise, the sign of the result is the sign of x / y. Precision mode has no effect on the remainder functions.

remquo returns n in the parameter n.

Special Values
x	y	remainder(x, y)	n	invalid?
±0.0	not 0.0	±0.0	0.0	no
±∞	anything	NAN	?	yes
anything	±0.0	NAN	?	yes
!= ±∞	±∞	x	?	no

Note:
remquo not supported on windows

int isnan(real x);

Returns !=0 if e is a NaN.

int isfinite(real e);

Returns !=0 if e is finite (not infinite or NAN).

int isnormal(X)(X x);

Returns !=0 if x is normalized (not zero, subnormal, infinite, or NAN).

int issubnormal(float f); int issubnormal(double d); int issubnormal(real x);

Is number subnormal? (Also called "denormal".) Subnormals have a 0 exponent and a 0 most significant mantissa bit.

int isinf(real x);

Return !=0 if e is ±∞.

bool isIdentical(real x, real y);

Is the binary representation of x identical to y?

Same as ==, except that positive and negative zero are not identical, and two NANs are identical if they have the same 'payload'.

int signbit(real x);

Return 1 if sign bit of e is set, 0 if not.

real copysign(real to, real from);

Return a value composed of to with from's sign bit.

real nan(char[] tagp);

Creates a quiet NAN with the information from tagp[] embedded in it.

BUGS:
DMD always returns real.nan, ignoring the payload.

real nextUp(real x); double nextUp(double x); float nextUp(float x);

Calculate the next largest floating point value after x.

Return the least number greater than x that is representable as a real; thus, it gives the next point on the IEEE number line.

Special Values
x	nextUp(x)
-∞	-real.max
±0.0	real.min*real.epsilon
real.max	∞
∞	∞
NAN	NAN

Remarks:
This function is included in the forthcoming IEEE 754R standard.

real nextDown(real x); double nextDown(double x); float nextDown(float x);

Calculate the next smallest floating point value before x.

Return the greatest number less than x that is representable as a real; thus, it gives the previous point on the IEEE number line.

Special Values
x	nextDown(x)
∞	real.max
±0.0	-real.min*real.epsilon
-real.max	-∞
-∞	-∞
NAN	NAN

Remarks:
This function is included in the forthcoming IEEE 754R standard.

real nextafter(real x, real y); float nextafter(float x, float y); double nextafter(double x, double y);

Calculates the next representable value after x in the direction of y.

If y > x, the result will be the next largest floating-point value; if y < x, the result will be the next smallest value. If x == y, the result is y.

Remarks:
This function is not generally very useful; it's almost always better to use the faster functions nextUp() or nextDown() instead.

IEEE 754 requirements not implemented on Windows: The FE_INEXACT and FE_OVERFLOW exceptions will be raised if x is finite and the function result is infinite. The FE_INEXACT and FE_UNDERFLOW exceptions will be raised if the function value is subnormal, and x is not equal to y.

real fdim(real x, real y);

Returns the positive difference between x and y.

Returns:

Special Values
x, y	fdim(x, y)
x > y	x - y
x <= y	+0.0

real fmax(real x, real y);

Returns the larger of x and y.

real fmin(real x, real y);

Returns the smaller of x and y.

real fma(real x, real y, real z);

Returns (x * y) + z, rounding only once according to the current rounding mode.

BUGS:
Not currently implemented - rounds twice.

real pow(real x, uint n); real pow(real x, int n);

Fast integral powers.

real pow(real x, real y);

Calculates xy.

Special Values
x	y	pow(x, y)	div 0	invalid?
anything	±0.0	1.0	no	no
\|x\| > 1	+∞	+∞	no	no
\|x\| < 1	+∞	+0.0	no	no
\|x\| > 1	-∞	+0.0	no	no
\|x\| < 1	-∞	+∞	no	no
+∞	> 0.0	+∞	no	no
+∞	< 0.0	+0.0	no	no
-∞	odd integer > 0.0	-∞	no	no
-∞	> 0.0, not odd integer	+∞	no	no
-∞	odd integer < 0.0	-0.0	no	no
-∞	< 0.0, not odd integer	+0.0	no	no
±1.0	±∞	NAN	no	yes
< 0.0	finite, nonintegral	NAN	no	yes
±0.0	odd integer < 0.0	±∞	yes	no
±0.0	< 0.0, not odd integer	+∞	yes	no
±0.0	odd integer > 0.0	±0.0	no	no
±0.0	> 0.0, not odd integer	+0.0	no	no

int feqrel(X)(X x, X y);

To what precision is x equal to y?

Returns:
the number of mantissa bits which are equal in x and y. eg, 0x1.F8p+60 and 0x1.F1p+60 are equal to 5 bits of precision.

Special Values
x	y	feqrel(x, y)
x	x	real.mant_dig
x	>= 2*x	0
x	<= x/2	0
NAN	any	0
any	NAN	0

real poly(real x, real[] A);

Evaluate polynomial A(x) = a₀ + a₁x + a₂² + a₃x³ ...

Uses Horner's rule A(x) = a₀ + x(a₁ + x(a₂ + x(a₃ + ...)))

Params:

real[] A

array of coefficients a₀, a₁, etc.